一天一招平行四邊形的特征，今天我們又來學(xué)習(xí)平行四邊形。 你好，上節(jié)課我們學(xué)習(xí)了平行四邊形的定義和性質(zhì)，你還記得嗎？ 讓我們沿著記憶之路走一趟。

平行四邊形的定義：兩條對(duì)邊平行的四邊形稱為平行四邊形。 平行四邊形的性質(zhì)：

·1. 邊數(shù)：平行四邊形的兩條相對(duì)邊相等。

·2. 角：平行四邊形的兩個(gè)對(duì)角相等。

·3. 對(duì)角線：平行四邊形的對(duì)角線互相平分。

我們知道，研究幾何圖形的總體思路是首先給出圖形的定義，然后研究圖形的性質(zhì)，最后探索確定圖形的條件。 在本課中，我們將探討確定平行四邊形的方法。

你知道如何證明四邊形是平行四邊形嗎？ 首先，根據(jù)定義，如果已知四邊形的兩條對(duì)邊平行，則該四邊形是平行四邊形。 除了定義之外還有其他方法可以判斷嗎？ 你還記得我們?cè)谏弦徽聦W(xué)習(xí)勾股定理時(shí)也有過類似的經(jīng)歷嗎？

如果已知三角形是直角三角形，則可以發(fā)現(xiàn)三邊之間的關(guān)系是平方a加平方b等于平方c。 另一方面，如果已知三角形的三邊滿足平方a加平方b等于平方c，則可以證明該三角形是直角三角形。 因此，直角三角形的判定定理是性質(zhì)定理的逆命題。

我們是否從中得到一些啟發(fā)呢？ 基于性質(zhì)定理的逆命題可以研究平行四邊形的判定方法。 請(qǐng)看表并要求你猜測(cè)如何根據(jù)平行四邊形的性質(zhì)確定它。

·你猜第一句是什么？ 你說得很好，兩條邊相等的四邊形是平行四邊形。

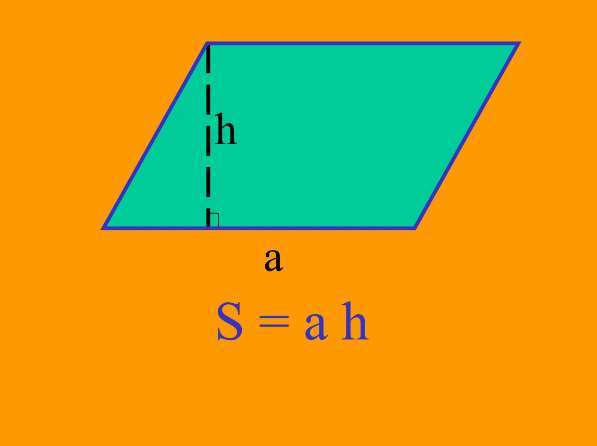
·第二行兩個(gè)對(duì)角相等的四邊形是平行四邊形。

·你猜第三行的內(nèi)容是什么？ 對(duì)角線互相平分的四邊形是平行四邊形。

如果原命題正確，那么逆命題就一定正確嗎？ 不一定正確。 我們的猜測(cè)是否正確，需要邏輯推理來判斷。 你能證明上面的猜想嗎？

本課以第三個(gè)猜想為例進(jìn)行證明。 請(qǐng)你自己完成另外兩個(gè)猜想。 接下來請(qǐng)用文字描述對(duì)角線互相平分的四邊形是平行四邊形，畫出圖形并寫出已知的驗(yàn)證和證明過程。 你寫完了嗎？

我們先一起來看一下畫面。 如圖所示，在四邊形ABCD中，AC和BD交于O點(diǎn)，且OA=OC，OB=OD。 驗(yàn)證四邊形 ABCO 是平行四邊形。 如何證明四邊形是平行四邊形？ 根據(jù)定義，相對(duì)的兩條邊可以平行。

如何證明對(duì)邊平行？ 證明兩條直線平行的常用方法是通過角度關(guān)系。 如何證明兩個(gè)角相等？ 你說的非常好。 這可以通過已研究的三角形的全等來證明。 你能找出圖中哪兩個(gè)三角形全等嗎？ 是的，三角形A00全等于三角形COB平行四邊形的特征，三角形AOB全等于三角形COB。

為什么它們是一致的？ 我們來看看具體的寫證明過程。 證明：OA=OC，OB=OD，AOD=COB，△AOD=△COB。（SAS）。 角A00等于角COB，且對(duì)角頂角相等，因此三角形A00等于三角形COB。 原因是Sas，所以角口AO等于角OCB。 若內(nèi)角相等，則可證明AD與BC平行。

同理，A8與CO平行，所以四邊形ABCO是平行四邊形。 這證明對(duì)角線互相平分的四邊形是平行四邊形。

在本課中，我們學(xué)習(xí)了確定平行四邊形的四種方法：定義和三個(gè)確定定理。 請(qǐng)記住這些方法。 今天的課程就到此為止。 再見。