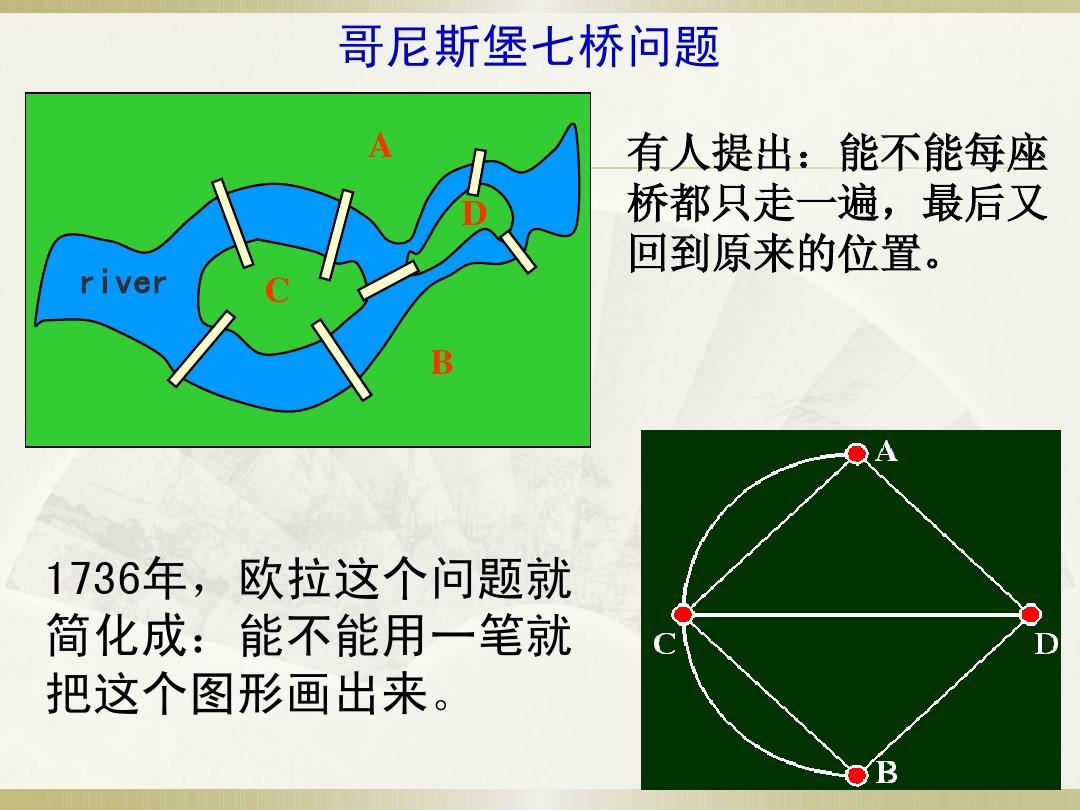
這個抽象的過程很重要，這種抽象思維對于學好數學很重要，也許你用鉛筆尖在圖畫上畫畫，做實驗，很好，你做的很好。為什么這么說呢？因為你在做這件事情的時候，你運用了想象力：你不經意間把自己想象成一個小筆尖，你用筆尖在七座橋的圖畫上畫畫，把它想象成你自己的經歷。一位教育家曾經說過“強大而活躍的想象力是大智慧不可缺少的屬性”。看來你并不缺乏這種想象力。我們再想想七橋問題一筆畫答案，剛才你用筆尖在七座橋的圖畫上畫畫，把它想象成你自己過橋的經歷，這不是把過橋的問題和畫一筆的問題聯系起來了嗎？用一句數學的俗話來說，這就是把現實生活中的問題轉化為數學問題。下圖詳細描繪了這個轉化過程。 下頁左圖中，將陸地想象成分成幾大塊。這并不影響過橋問題的解決。下頁右圖中，將陸地塊進一步縮小，用一條線段來表示小橋。這并不改變過橋問題的本質。下圖左圖中，將陸地和島嶼進一步用小圓圈表示。這已經是一個“幾何圖形”，但看上去還是很復雜。下圖右圖中，將圓圈進一步縮小為一個點。這樣，就變成了最簡單的僅由點和線構成的幾何圖形。經過上述簡化，七座橋問題確實變成了上圖右圖（即第5講練習1中的圖（9））能否一筆畫出來的問題。

很容易看出，圖中有4個奇點，根據上一講得到的判斷規則可知，它無法一筆畫出來，所以人不可能一次連續走過七座橋。這樣，七座橋問題就被完美解決了，這個解法是大數學家歐拉找到的。這種簡化，也是一種抽象的過程，所謂“抽象”，就是在解決實際問題的過程中，把一切與問題無關的方面都舍棄掉，只抓住那些能夠反映問題本質的東西。就好比在七座橋問題中，陸地和島嶼的大小，橋梁的寬度和長度，都是與問題無關的。最后，我們來總結一下解決七座橋問題的要點： ? 將陸地和島嶼化簡為點，將橋梁畫成線，這樣，原圖就變成了簡單的幾何圖形。 ? 如果這個由點和線組成的圖形是一筆畫出來的，人們一次可以走過所有的橋；如果這個圖形不能一筆畫出來，人們就不能一次通過所有的橋。？根據上面的判斷規則，具有0個或2個奇異點的圖形是一筆畫出來的，如果奇異點多于2個，則該圖形不能一筆畫出來。仿照這個思想，還可以解決很多類似的問題。練習6 1、學習歐拉，先把過橋問題轉化為一筆畫出來的問題，然后進行判斷（見下圖）。過橋問題：你能否過橋一次（每座橋只能過一次），按照這個例子依次判斷：2、下圖是鄉村里的一條小河，河上建有6座橋，你能一次性不重復地走完所有的小橋嗎？（每座小橋最多只能過一次，陸地上可以反復來回走）3.

在我國著名數學家陳景潤所著的《數學趣事》一書中，有一道題是這樣的。大意是：在法國首都巴黎有一條河流，河中有兩個小島。人們修建了15座橋把兩個小島與河岸連接起來，如下圖所示。請告訴我，從任意一岸出發，能否一次性通過所有橋到達對岸？（每座橋只能走一次） 4、下圖是一個售樓處。問顧客從入口進去時，是否可以不走重復路，穿過所有的門，請說明你的理由。 假如售樓處的出口在4號房間，你設計了另一扇門，讓顧客從入口進去后可以不走重復路，再從4號房間去售樓處，你打算把另一扇門開在哪里？ 練習6 答案 1.解答：參見下圖 過橋問題：能否一次性通過所有的橋（每座橋只能走一次） 一筆畫圖問題：能否一筆畫出一個圖形（不能抬筆，不能重復） 2.解答：參見下面兩張圖，可以看到不能一次性不重復地走完所有的橋，因為下圖中有4個奇異點。 3.解答：由于經過兩個島中任意一處的橋數都是偶數，而經過兩岸任意一處的橋數都是奇數，這就意味著從任意一岸出發，都有一條路可以讓人只走完所有的橋一次，到達對岸。畫一張圖就一目了然了。參見下圖，因為圖中有兩個奇異點，奇異點都是兩岸，所以是一筆畫圖。 這樣人們就可以一次穿過所有的橋，每座橋只需走一次七橋問題一筆畫答案，就能從一岸到達另一岸。

4、解答：從入口進入售樓處之后，也就是從1號房間出發，不重復是無法走過所有的門的英語作文網，因為雖然整個圖（見下圖）只有2個奇異點，但是點1是偶數點，當出口是4號房間時，如果在1號房間和3號房間之間再開一扇門，那么從1開始，因為點1變成了奇異點，所以從4號房間出發之后不重復是無法走過所有的門的，但是點1仍然是奇異點，而整個圖只有2個奇異點，所以可以從1號房間進入，從4號房間出去，見下圖（進入售樓處之后可以先從1號房間進入3號房間）。