綜觀近幾年的中考語文試題，我們會發(fā)覺與雙曲線相關(guān)的題型幾乎年年就會考到，屬于重要考點。題型也比較豐富，如有選擇題、填空題、解答題的方式；考查的知識點有雙曲線的定義、標(biāo)準(zhǔn)多項式、漸近線和離心律、雙曲線的性質(zhì)、直線與雙曲線的位置關(guān)系等等。

跟雙曲線有關(guān)的選擇題或填空題通常分值為4分或5分，解答題甚至10分題目就會有。為此，考生對雙曲線的學(xué)習(xí)應(yīng)加以注重。

要想學(xué)好雙曲線，我們可以“借用”其他幾個圓柱曲線內(nèi)容，如學(xué)習(xí)雙曲線的定義、標(biāo)準(zhǔn)多項式和幾何性質(zhì)時，可以對橢圓的定義、標(biāo)準(zhǔn)多項式和幾何性質(zhì)進(jìn)行類比，找出它們的不同點，對比記憶，加深理解。

橢圓的定義：

平面內(nèi)到兩個定點F1，F(xiàn)2的距離之和等于常數(shù)(小于|F1F2|)的點的軌跡稱作橢圓，這兩個定點稱作橢圓的焦點，兩焦點F1，F(xiàn)2間的距離稱作橢圓的焦距。

雙曲線的定義：

平面內(nèi)與定點F1、F2的距離的差的絕對值等于常數(shù)(大于|F1F2|)的點的軌跡稱作雙曲線，這兩個定點稱作雙曲線的焦點，兩焦點間的距離稱作雙曲線的焦距。

從橢圓和雙曲線的定義，我們可以看見兩種知識的聯(lián)系和區(qū)別，這也更好幫助我們理解和把握好知識內(nèi)容。如要注意“常數(shù)”所滿足的條件以及絕對值所起的作用,要注意與橢圓中的有關(guān)多項式進(jìn)行比較,并加以區(qū)別。

典型例題剖析1：

已知雙曲線的多項式是16x2－9y2＝144.

(1)求雙曲線的焦點座標(biāo)、離心律和漸近線多項式；

(2)設(shè)F1和F2是雙曲線的左、右焦點，點P在雙曲線上，且|PF1|·|PF2|＝32，求∠F1PF2的大小．

解：(1)由16x2－9y2＝144得x2/9－y2/16＝1，

所以a＝3，b＝4，c＝5，

所以焦點座標(biāo)F1(－5,0)，F(xiàn)2(5,0)，離心律e＝5/3，漸近線多項式為y＝±4x/3.

(2)由雙曲線的定義可知||PF1|－|PF2||＝6，

cos∠F1PF2＝（|PF1|2+|PF2|2-|F1F2|2）/2|PF1||PF2|

＝{（|PF1|2-|PF2|）2+2|PF1||PF2|-|F1F2|2}/2|PF1||PF2|

＝（36+64-100）/64＝0，

則∠F1PF2＝90°.

要想正確解決雙曲線的問題，首先學(xué)好雙曲線的基本概念、知識點等等，如求雙曲線多項式時,若不能確定焦點位置,要注意分類討論.若焦點所在的座標(biāo)軸不同,其漸近線多項式的方式也不同。

分辨雙曲線與橢圓中a、b、c的關(guān)系，在橢圓中a2＝b2＋c2，而在雙曲線中c2＝a2＋b2.雙曲線的離心律e＞1；橢圓的離心律e∈(0,1)。

典型例題剖析2：

設(shè)F1漸近線的定義，F(xiàn)2是雙曲線x2－y2/24＝1的兩個焦點，P是雙曲線上的一點，且3|PF1|＝4|PF2|，則△PF1F2的面積等于.

解析：由P是雙曲線上的一點和3|PF1|＝4|PF2|可知漸近線的定義，|PF1|－|PF2|＝2，解得|PF1|＝8，|PF2|＝6.又|F1F2|＝2c＝10，所以△PF1F2為直角三角形，所以△PF1F2的面積S＝(6×8)/2＝24。

雙曲線作為中考的熱點內(nèi)容之一，在每年全省各地的中考試題中，就會有相關(guān)的題型出現(xiàn)。一些復(fù)雜題型會以直線與雙曲線位置關(guān)系為背景的求雙曲線多項式問題，要借助點差法處理弦中點與斜率問題等。

應(yīng)用雙曲線的定義需注意的問題：

在雙曲線的定義中要注意雙曲線上的點(動點)具備的幾何條件，即“到兩定點(焦點)的距離之差的絕對值為一常數(shù)，且該常數(shù)必須大于兩定點的距離”。若定義中的“絕對值”去掉，點的軌跡是雙曲線的一支。

典型例題剖析3：

牢記：雙曲線多項式的求法

1、若不能明晰焦點在哪條座標(biāo)軸上，設(shè)雙曲線多項式為mx2＋ny2＝1(mn

2、與雙曲線x2/a2－y2/b2＝1有共同漸近線的雙曲線多項式可設(shè)為x2/a2－y2/b2＝λ(λ≠0)；

3、若已知漸近線多項式為mx＋ny＝0，則雙曲線多項式可設(shè)為m2x2－n2y2＝λ(λ≠0)。

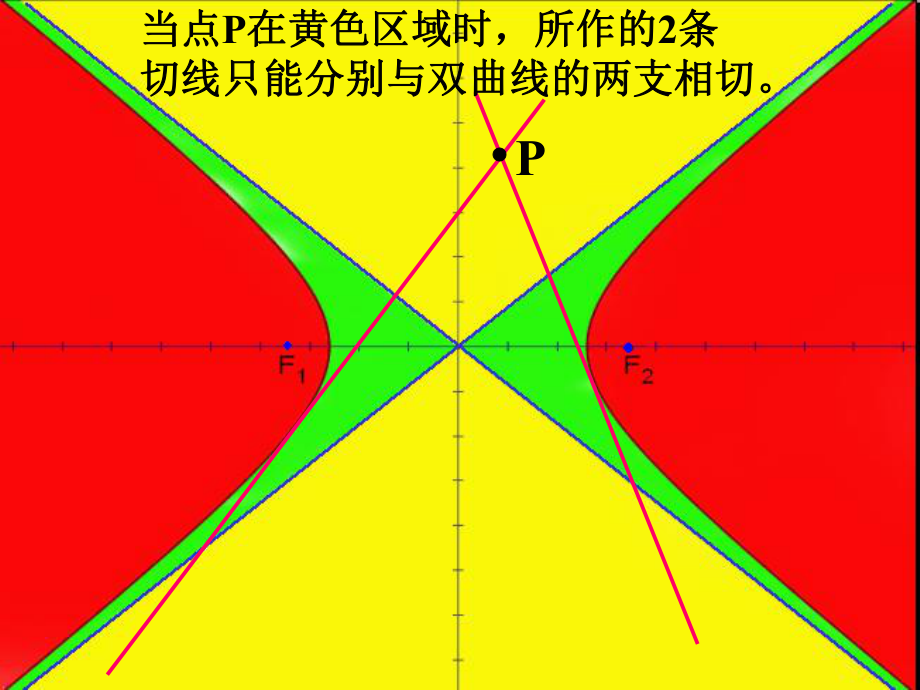
直線與雙曲線交于一點時，不一定相切，如：當(dāng)直線與雙曲線的漸近線平行時，直線與雙曲線相交于一點，但不是相切；反之，當(dāng)直線與雙曲線相切時，直線與雙曲線僅有一個交點。

典型例題剖析4：

要學(xué)會設(shè)出直線多項式或雙曲線多項式，之后把直線多項式和雙曲線多項式組成多項式組，消元后轉(zhuǎn)化成關(guān)于x(或y)的一元二次方程。

借助根與系數(shù)的關(guān)系，整體代入。

與中點有關(guān)的問題常用點差法。

要學(xué)會依照直線的斜率k與漸近線的斜率的關(guān)系來判定直線與雙曲線的位置關(guān)系。

對于雙曲線綜合類問題，通常還會考查到雙曲線的標(biāo)準(zhǔn)多項式、待定系數(shù)法、直線多項式、直線與雙曲線的位置關(guān)系等知識，這種題型綜合性強，估算量大。