圓心定理:三角形三邊的垂直平分線相交于一點。 該點稱為三角形的外心。
注意,外心到三角形三個頂點的距離相等,結合垂直平分線的定義,外心定理其實很容易證明。
計算外心重心坐標是一項麻煩的工作。 首先計算以下臨時變量:
d1、d2和d3分別是連接三角形的三個頂點到另外兩個頂點的向量的點積。
c1=d2d3, c2=d1d3, c3=d1d2; c=c1+c2+c3。
重心坐標:((c2+c3)/2c、(c1+c3)/2c、(c1+c2)/2c)。
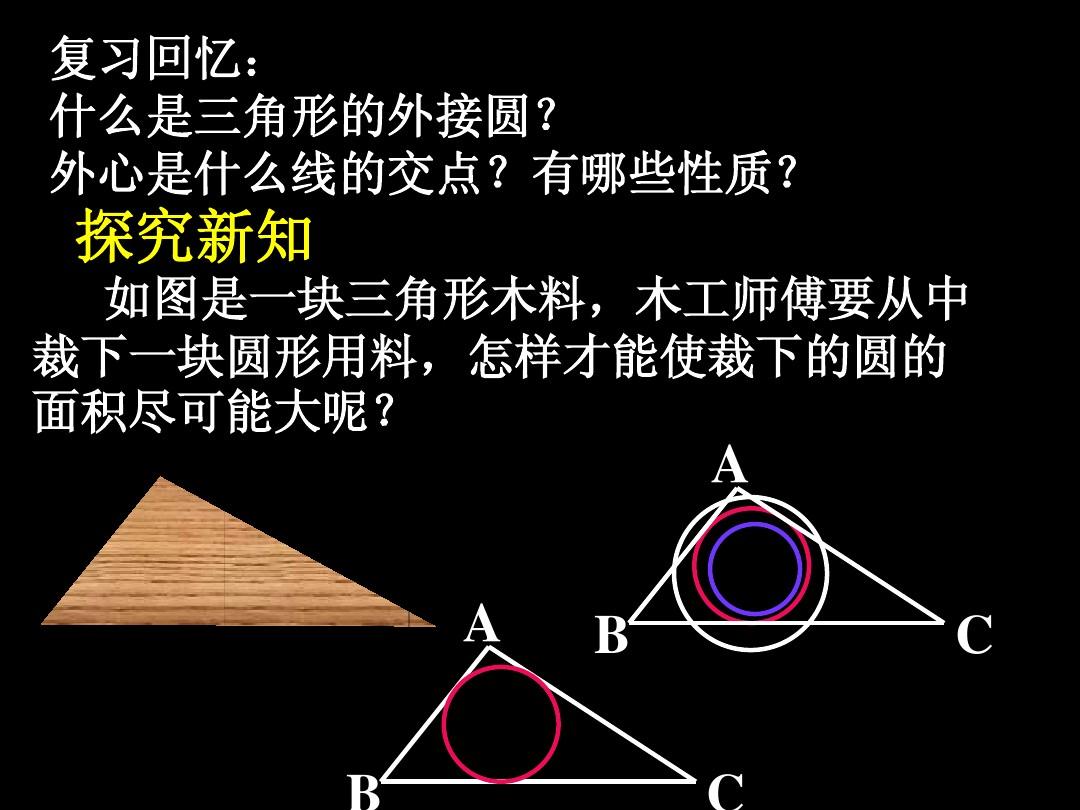
圓心是三角形三個內角平分線的交點,也就是內切圓的圓心。
圓心為三角形角平分線交點的原理:過圓外一點畫兩條切線,連此點與圓心的連線平分兩條切線之間的角度(原理:角平分線上的點到角兩邊的距離相等)。
內定理:三角形三個內角的平分線相交于一點。 該點稱為三角形的內心。

注意,圓心到三邊的距離相等(內切圓的半徑),圓心定理其實很容易證明。
若三邊分別為l1、l2、l3,周長為p,則重心坐標為(l1/p,l2/p,l3/p)。
直角三角形的心到邊的距離等于兩個直角邊之和減去斜邊之差的二分之一。
雙曲線任意分支上的一點與兩個焦點所形成的三角形的中心在實軸上的投影就是相應分支的頂點。
重心是三角形三邊中心線的交點。 三條線的交點可以用燕尾定理證明,很簡單。 證明過程又是 Ceva 定理的一個特例。
重心的幾個性質:
1、重心到頂點的距離與重心到對邊中點的距離之比為2:1。
2、重心與三角形三個頂點組成的三個三角形的面積相等。

3、重心到三角形三個頂點的距離的平方和最小。
4、在平面直角坐標系中,重心坐標為頂點坐標的算術平均值,即其坐標為((X1+X2+X3)/3,(Y1+Y2+Y3)/ 3); 空間直角坐標系——橫坐標:(X1+X2+X3)/3 縱坐標:(Y1+Y2+Y3)/3 縱坐標:(z1+z2+z3)/3
三角形三個高的交點稱為三角形的垂線。
銳角三角形的重心在三角形內部。
直角三角形的重心位于三角形的頂點。
鈍角三角形的重心在三角形的外面。
垂直中心為高線的交點
垂線是從三角形的頂點到其對邊所畫的三個垂線的交點。
三角形的三個頂點、三個垂直腳和垂直中心可以產生6個四點圓。
在三角形上畫三個高,三個高必須相交于垂直中心。
高線將三角形分開,出現三對直角。
有十二個直角三角形,形成六對相似的形狀。
有一個四點圓圖外心的性質和定義,仔細分析就可以發現。
證明如第二張圖所示。 雖然“角”符號是亂碼,但是大家應該都能看懂。 CF為待證明的高度; 兩個角度(DOC和BAD)相等后使用相似性證明外心的性質和定義,這部分省略。 對于直角三角形,直角的頂點顯然是垂直中心; 鈍角——你沒發現三角形OBC的垂直中心是A嗎?
垂直中心的重心坐標比外心的重心坐標簡單。 首先計算以下臨時變量(與外心相同):
d1、d2、d3是連接三角形三個頂點到另外兩個頂點的向量的點積(這句話很長^_^)。
c1=d2d3, c2=d1d3, c3=d1d2; c=c1+c2+c3。
重心坐標:(c1/c、c2/c、c3/c)。
 名師輔導
環球網校
建工網校
會計網校
新東方
醫學教育
中小學學歷
名師輔導
環球網校
建工網校
會計網校
新東方
醫學教育
中小學學歷